Assuming a regular polygon consisting of 8 points and 8 "dents", the figure would seem to be one of the following. (The 200° angle is marked with an arc.)
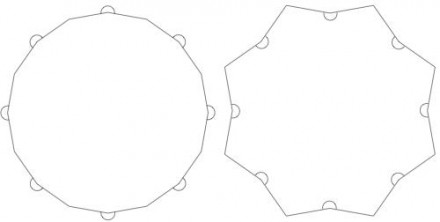Either way, the "dent" seems to look a lot like a "point".
If dents and points are measured as internal angles (as on the right), the sum of a dent-point pair will be 14/8*180° = 315°. Thus, a "dent" angle will be 115°.
If dents and points are measured on the outside (as on the left), the corresponding sum of each dent-point pair will be 360°(1+1/8) = 405°. Thus, a "dent" angle will be 205°.
Of course, the concave angle in the figure on the right is 360° - 200° = 160°.
Perhaps you mean the point angle is 20°. Then the figure would look like this.
The interior "dent" angle is 315° - 20° = 295°, so the exterior dent angle is 65°.
If dents and points are measured as internal angles (as on the right), the sum of a dent-point pair will be 14/8*180° = 315°. Thus, a "dent" angle will be 115°.
If dents and points are measured on the outside (as on the left), the corresponding sum of each dent-point pair will be 360°(1+1/8) = 405°. Thus, a "dent" angle will be 205°.
Of course, the concave angle in the figure on the right is 360° - 200° = 160°.
Perhaps you mean the point angle is 20°. Then the figure would look like this.
