It is hard to give an answer when there is no question.
Here is a PowerPoint file that shows the method step by step. The name of the method appears to derive from the peculiar shape of bracket used to separate the quotient and its arithmetic from the computation and subtraction associated with the dividend.
The method shown in the file has you make any sort of guess as to the highest quotient digit, then multiply and subtract in the usual way for long division. If you guessed a little low, that's OK because in the end you just add up the partial quotient values.
At the bottom, you will have a remainder. This method does not lend itself well to determining decimal equivalents of fractions, for example, unless you extend the dividend to the right before you start.
The graphic below shows 1 completed "guess" and a second "guess" at the quotient with work in progress. Each quotient guess is multiplied by the divisor and subtracted from the current dividend to get a new dividend. Quotient guesses are noted to the right of the vertical bar.
At then end, when the remaining dividend is smaller than the divisor, you add the quotient guesses to get the final quotient answer. The remaining dividend value is the remainder of the division operation.
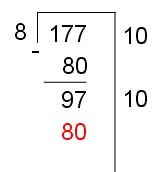The next step in the problem shown is to subtract 80 from 97 to get 17. Now make a guess as to the number of times 8 will go into 17. It will be 2, so we write 2 to the right of the vertical line, and compute 2*8 = 16. Subtracting 16, we get the remainder of 1. Adding the partial quotients on the right, we get 10+10+2 = 22. We have computed 177/8 = 22 remainder 1.
Here is a PowerPoint file that shows the method step by step. The name of the method appears to derive from the peculiar shape of bracket used to separate the quotient and its arithmetic from the computation and subtraction associated with the dividend.
The method shown in the file has you make any sort of guess as to the highest quotient digit, then multiply and subtract in the usual way for long division. If you guessed a little low, that's OK because in the end you just add up the partial quotient values.
At the bottom, you will have a remainder. This method does not lend itself well to determining decimal equivalents of fractions, for example, unless you extend the dividend to the right before you start.
The graphic below shows 1 completed "guess" and a second "guess" at the quotient with work in progress. Each quotient guess is multiplied by the divisor and subtracted from the current dividend to get a new dividend. Quotient guesses are noted to the right of the vertical bar.
At then end, when the remaining dividend is smaller than the divisor, you add the quotient guesses to get the final quotient answer. The remaining dividend value is the remainder of the division operation.