Initially 50 pounds of salts is dissolved in a large tank having 300 gallons of water. A brine solution is pumped into the tank at a rate of 3 gal/min and a well-stirred solution is then pumped out at the same rate?

Suppose the total amount of salts in the tank is s[t] pounds, where t is time in minutes. We are told that
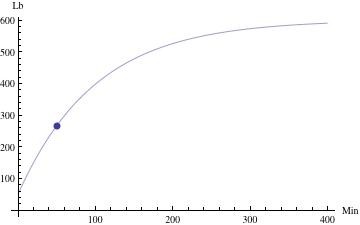
  s[0] = 50 pounds
The rate of increase of s[t] is
  (3 gal/min)*(2 lb/gal) = 6 lb/min
The rate of decrease of s[t] (in pounds per minute) is
  s/(300 gal)*(3 gal/min)
Expressing these relationships using a differential equation, we have
  s'[t] = 6 - (1/100)*s,
  s[0] = 50
We recognize that the solution to this linear non-homogeneous equation with constant coefficients will be of the form
  s[t] = c₁e^(a*t) + c₀  for some values of a and constants c_n.
Substituting this into the differential equation above, and matching coefficients, we get
  c₁*a*e^(a*t) = 6 - (1/100)*c₁*e^(a^t) - (1/100)*c₀   c₁*a = -(1/100)*c₁    (match coefficients of e^(a*t))
  a = -1/100   0 = 6 - (1/100)*c₀    (match constants)
  c₀ = 600   c₁*e^(-0/100) + 600 = 50    (evaluate for initial condition)
  c₁ = 50 - 600 = -550 The salt quantity is
  s[t] = 600 - 550e^(-t/100)) After 50 minutes, the salt quantity in the tank will be
  s[50] = 600 - 550*e^(-1/2)
  s[50] ≈ 266.4 pounds of salts The quantity present as t gets very large will be
  s[infinity] = 600 pounds