The signs of the terms are + - + -, so there are 3 changes of sign. By Descartes' rule of signs, that means there are 3 (or 1) positive real roots. It also means there are 0 or 2 possible imaginary roots.
The derivative is
F'(x) = 6x^2 - 8x + 8
The discriminant of this expression is (-8)^2 - 4(6)(8) = 64 - 192 = -128.
This means the derivative expression F'(x) is positive for all values of x, so the slope of the expression F(x) is positive for all values of x. There will be 2 imaginary zeros of F(x).
Here's the graph of F(x).
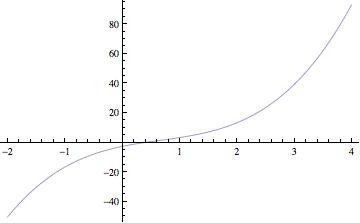
The derivative is
F'(x) = 6x^2 - 8x + 8
The discriminant of this expression is (-8)^2 - 4(6)(8) = 64 - 192 = -128.
This means the derivative expression F'(x) is positive for all values of x, so the slope of the expression F(x) is positive for all values of x. There will be 2 imaginary zeros of F(x).
Here's the graph of F(x).
