Given a cubic equation of the form ax3+bx2+cx+d=0, an annoyingly complicated formula for the "discriminant" will tell you how many real roots the equation has. The discriminant is 18abcd-4(ac3+b3d)+b2c2-27a2d2. If it is <0, there are two complex roots and one real root. If it is =0, all roots are real and at least two of them are equal. If the discriminant is >0, there are three unequal real roots.
Another quick, but not so comprehensive, test is to look at b2-3ac. If this value is <0, the equation has only one real root. If this value is =0 or >0, something can be said about the number of inflection points in the graph of ax3+bx2+cx+d, but that is all.
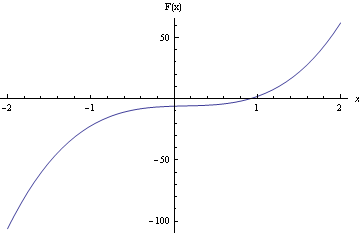
So, in your F(x) = 10x3 - 4x2 + 2x - 6, the value of b2-3ac is (-4)2-3(10)(2)=16-60=-44. Thus, the function F(x) is monotonic (has no inflection points) and there is only one real root. The other two roots must be complex, i.e. They have a non-zero imaginary part.
Another quick, but not so comprehensive, test is to look at b2-3ac. If this value is <0, the equation has only one real root. If this value is =0 or >0, something can be said about the number of inflection points in the graph of ax3+bx2+cx+d, but that is all.
So, in your F(x) = 10x3 - 4x2 + 2x - 6, the value of b2-3ac is (-4)2-3(10)(2)=16-60=-44. Thus, the function F(x) is monotonic (has no inflection points) and there is only one real root. The other two roots must be complex, i.e. They have a non-zero imaginary part.
