The regula falsi method is an iterative method of root finding that uses a linear approximation of the function between functional values of opposite sign known to bracket the root. It is also known as the secant method.
The first step is to find values of the independent variable for which values of the function have opposite sign. Descartes' Rule of Signs and the Rational Root Theorem can be helpful in this.
For your function
f(x) = x^3 + x - 3
There is one change of sign, so one positive root. Possible rational roots include 1 or 3. Evaluating the function for these values, we have f(1) = -1, f(3) = 27, so the root lies in the open interval (1, 3). A check that f(2) = 7 can help us narrow the starting range to the interval (1, 2).
The next step is to perform the iteration. We can use as the iteration formula
x = x1 - (x2 - x1)/(y2 - y1)*y1
where x1 and x2 are chosen such that y1=f(x1) and y2=f(x2) have opposite signs and one of them is the most recent value of x.
We start with (x1, y1) = (1, -1) and (x2, y2) = (2, 7). Our next value of x will be
x = 1 - (2 - 1)/(7 - (-1))*(-1) = 1 - (1/8)*(-1) = 9/8
We find that f(9/8) = -(231/512) < 0, so our new (x1, y1) is (9/8, -231/512).
Repeating the iteration, we find convergence is fairly slow. Here are the (x1, x2) values for the first 9 iterations. We see that the last iterations have changes in the 4th decimal place. The value of f(x1) at that point is -0.000107134, perhaps close enough to zero for what you want.
{1., 2.}, {1.125, 2.}, {1.17798, 2.}, {1.19941, 2.}, {1.20791, 2.},
{1.21126, 2.}, {1.21257, 2.}, {1.21308, 2.}, {1.21328, 2.},
{1.21336, 2.}, {1.21339, 2.}
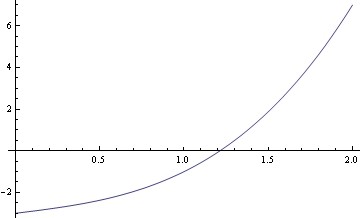My root finder gives the root as 1.21341.
The first step is to find values of the independent variable for which values of the function have opposite sign. Descartes' Rule of Signs and the Rational Root Theorem can be helpful in this.
For your function
f(x) = x^3 + x - 3
There is one change of sign, so one positive root. Possible rational roots include 1 or 3. Evaluating the function for these values, we have f(1) = -1, f(3) = 27, so the root lies in the open interval (1, 3). A check that f(2) = 7 can help us narrow the starting range to the interval (1, 2).
The next step is to perform the iteration. We can use as the iteration formula
x = x1 - (x2 - x1)/(y2 - y1)*y1
where x1 and x2 are chosen such that y1=f(x1) and y2=f(x2) have opposite signs and one of them is the most recent value of x.
We start with (x1, y1) = (1, -1) and (x2, y2) = (2, 7). Our next value of x will be
x = 1 - (2 - 1)/(7 - (-1))*(-1) = 1 - (1/8)*(-1) = 9/8
We find that f(9/8) = -(231/512) < 0, so our new (x1, y1) is (9/8, -231/512).
Repeating the iteration, we find convergence is fairly slow. Here are the (x1, x2) values for the first 9 iterations. We see that the last iterations have changes in the 4th decimal place. The value of f(x1) at that point is -0.000107134, perhaps close enough to zero for what you want.
{1., 2.}, {1.125, 2.}, {1.17798, 2.}, {1.19941, 2.}, {1.20791, 2.},
{1.21126, 2.}, {1.21257, 2.}, {1.21308, 2.}, {1.21328, 2.},
{1.21336, 2.}, {1.21339, 2.}