The area enclosed over the region of interest will be the definite integral of this expression over the region of interest. The integral of
y = 16 - 4x - 4x^2 + x^3
is
g[x] = Integral[y] = 16x - 2x^2 - (4x^3)/3 + x^4/4
If the region of interest is x = {-2, 2}, the area evaluates to
g[2] - g[-2] = (52/3 - (-76/3)) = 128/3.
Please take a look at the picture.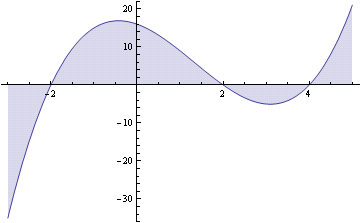
y = 16 - 4x - 4x^2 + x^3
is
g[x] = Integral[y] = 16x - 2x^2 - (4x^3)/3 + x^4/4
If the region of interest is x = {-2, 2}, the area evaluates to
g[2] - g[-2] = (52/3 - (-76/3)) = 128/3.
Please take a look at the picture.
