The circle centered at B is internally tangent to the circle centered at A. The smaller circle passes through the center of the larger circle and the length of AB is 5 units. If the smaller circle is cut out of the larger circle, how much of the area?

The question appears to be incomplete.
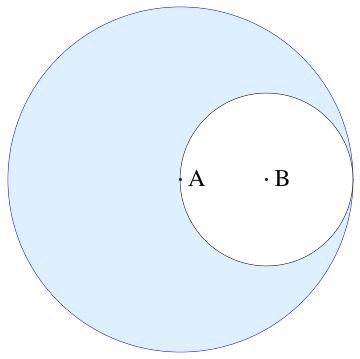
A picture helps. In each case the area measure is square units. The radius of the smaller circle is 5 units, so its area is
  a₀ = π*r^2 = 25π The radius of the larger circle is 10 units (the diameter of the smaller circle), so its area is
  a₁ = π*10^2 = 100π The remaining area of the larger circle, after the smaller circle is cut out, is
  a₁ - a₀ = π(100 - 25) = 75π