The points of discontinuity occur where the denominator goes to zero and changes sign.
A) 1-2sin[x] = 0
1 = 2sin[x]
1/2 = sin[x].
This will occur at x=(4n+1)Pi/2±Pi/3 radians = (4n+1)90±60 degrees, where n is any integer. See the picture.
B) There are no points of discontinuity, because the minimum magnitude the denominator may have is 3. It never goes to zero.
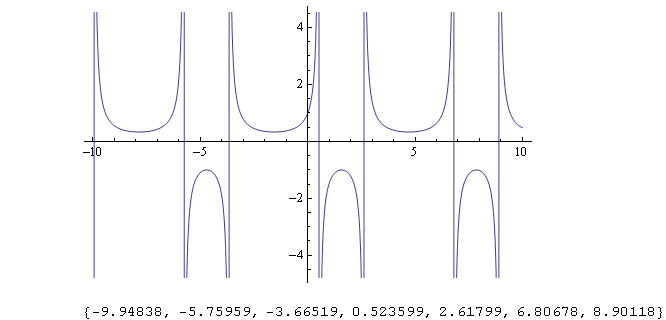
A) 1-2sin[x] = 0
1 = 2sin[x]
1/2 = sin[x].
This will occur at x=(4n+1)Pi/2±Pi/3 radians = (4n+1)90±60 degrees, where n is any integer. See the picture.
B) There are no points of discontinuity, because the minimum magnitude the denominator may have is 3. It never goes to zero.
