What three techniques can be used to solve a quadratic equation? Demonstrate all three techniques using the equation "9x2 + 3x - 6 = 0."

1.) Quadratic equation

2.) Completing the square

3.) Factor by grouping

Method 1 - The quadratic equation is:

To factor using this formula, you have to plug in numeric values for all three variables in the formula: A, b, and c. The numeric value for "a" is the number associated with the "x^2" variable. The numeric value for "b" is the number associated with the "x" variable. And the numeric value for "c" is the constant number that has no variable attached to it.

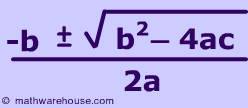
In the equation you have given, 9x^2 + 3x - 6 = 0, 9 represents a, 3 represents b, and -6 represents c. Simply plug in these three numbers into the equation, simplify, and you will get your x-solutions.

Method 2 - Completing the square

9x^2 + 3x = 6 (Add 6 to both sides)

x^2 + (x/3) = (2/3) (Divide both sides by 9)

x^2 + 2(x/6) = (2/3)

x^2 + 2(x/6) + (1/6)^2 = (2/3) + (1/6)^2 [Add (1/6)^2 to both sides]

(x + 1/6)^2 = 2/3 + 1/36 (Simplify)

(x + 1/6)^2 = 24/36 + 1/36

(x + 1/6)^2 = 25/36

Take the square root of both sides.

sqrt[(x + 1/6)^2] = sqrt(25/36)

x + 1/6 = 5/6 (Simplify)

x = 4/6 = 2/3 (Simplify further)

Method 3 - Factor by grouping

First, multiply the values of a and c together. In 9x^2 + 3x - 6 = 0, a = 9 and c = -6, so multiplying them together will give -54.

Now think, what factors of that number, -54, will sum up to the value of b, which is 3? (Taking the sum means to add). The factors are 9 and -6, because if you add them, you will get 3.

Think of 3x as 9x/5 and 6x/5 (because adding those two fractions together will give you 3x). So we can re-write the equation as:

9x^2 + 9x/5 + 6x/5 - 6

Now group the two pairs, and take out common terms from there. Observe:

(9x^2 + 9x/5) + (6x/5 - 6)

= 9x(x + 1/5) + 6(x/5 - 1)

= 9x(x + 1/5) + 1.2(x + 1/5)

You can see that there are two of (x + 1/5) there, with different constant numbers occurring before it. When you come across this, you must remove the common factors and rewrite as grouped factors:

(9x + 1.2)(x + 1/5)

Overall, method 1 is by far the easiest method to do. You just need to memorize a formula and plug in numbers, rather than do all this work for the other methods.