which basic trigonometric functions have vertical asymptotes?

Remember, vertical asymptotes occur when the denominator in a function is equal to zero.

By basic trig. Functions, I assume you mean sin/cos/tan.

Refer to this unit circle. When you have sine of a certain degree, you're measuring the y-value at that degree. So if you have f(x) = sin(90), pay close attention to where 90 degrees is on the unit circle. At the very top, right? And since sine measures the y-value at that degree, we can say that the value is 1 at 90 degrees. So sin(90) = 1.

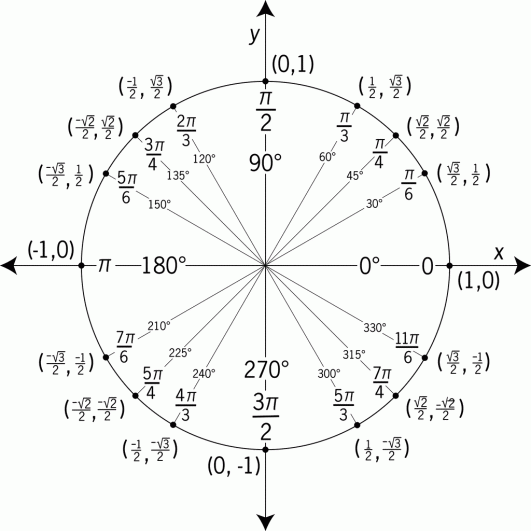
Cosine of a certain degree measures the x-value at that degree. So let's say we have f(x) = cos(60). Take a look on the unit circle where 60 degrees is located, and measure the x-value at that point. It would be 1/2, so we can say that cos(60) = 1/2.

Tangent of a certain degree measures the y-value divided by the x-value at that degree. If f(x) were to be tan(60), you would go look at the part of the unit circle where it says 60 degrees, and divide the y-value by the x-value, and that would be the answer for tan(60). In this case, tan(60) = [sqrt(3)/2]/(1/2) = sqrt(3)/1 = sqrt(3) which measures to about 1.73.

Now to get back to your question about vertical asymptotes. Like I said, the denominator has to be zero, and the numerator can be any number.

f(x) = tanx = sinx/cosx

If we plugged in 90 degrees for x, we would get:

f(90) = tan(90) = sin(90)/cos(90) = 1/0

The reason it came out to have a denominator of zero is because cosine measured at 90 degrees has zero as its value.

But wait a second...

f(270) = tan(270) = sin(270)/cos(270) = -1/0

There's more than one value that can make a basic trig function have a denominator of zero. And it's not just cosine. Sine and tangent can be zero at 0 degrees and 180 degrees.

So any basic trig function can have vertical asymptotes. It just has to be in the denominator and equal to zero.