Explain why you think the angle pairs formed by two lines and a transversal are related. Why might it be helpful to identify them as angles that go together instead of independent angles?

Question

Explain why you think the angle pairs formed by two lines and a transversal are related. Why might it be helpful to identify them as angles that go together instead of independent angles?

2 Answers

Answer Question

Answer 1

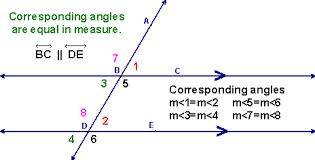
They're related in many ways.

A transversal is needed to make angle pairs, such as in this picture.

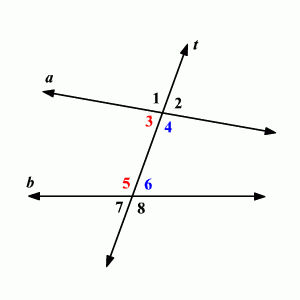
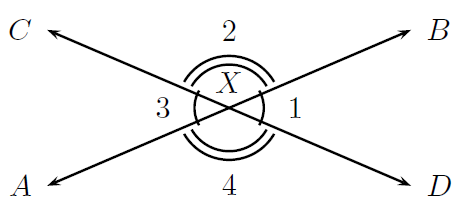
The transversal is clearly the line that's mostly vertical, compared to the other two lines. Without it, angle pairs couldn't be made. However, they can still be made without a tranversal, such as in this picture.

However, picture 1 shows more of how a transversal is related to angle pairs, because it's needed to actually make them!

Why might it be helpful to identify them as angles that go together instead of independent angles?

Let's take a look at the second picture. It shows that angles 1 and 3 are equal (by drawing one small arc next to either angle), as well as angles 2 and 4 being equal (by drawing two small arcs next to either angle). If we were asked to figure out exact angle degree measurement, using angle pairs here would save us 50% of the work. Let's say we found out the degree measurement for angle 1. Because of a rule of angle pairs, we can say that angle 3 has the same amount of degrees, already saving us 25% of the total work. If we do that same thing to angles 2 and 4, another 25% of the total work will be saved. That's why it's helpful to identify angle pairs as angles that go together rather than independent angles.

Answer 2

A transversal is a single line that crosses two or more other lines. These lines can be parallel but they do not need to be. This is one of the fundamental concepts of geometry.

The transversal creates an angle from, what would otherwise essentially be, two straight lines. When this happens, the angles formed are divided into pairs : Vertical angles, corresponding angles, alternate interior angles, alternate exterior angles and consecutive interior angles.

The only other way that two straight lines could form angles without the help of a transversal, is if the two lines crossed each other at some point.

It is helpful to identify angles in pairs, rather than independently, because we know that a group of angles created by a transversal share properties that make it easy to identify them. For example, the two angles 7 and 1 in the image above, together form a straight line - which tells us that the sum of their measurements must be 180 degrees.