A particle is moving along the ellipse 16x2 + 9y2 = 144. Find all points (x; y) on the ellipse at which the rates of change of x and y with respect to time are equal. (Assume that dx=dt and dy=dt are never both zero at the same point.)?

If x and y are functions of time (t), the derivative with respect to t is
  2*16*x*x' + 2*9*y*y' = 0
If x' = ±y', then
  ±16x + 9y = 0
  x = ±9y/16
Plugging this into the equation for the ellipse, we get
  16*(9/16y)^2 + 9*y^2 = 144
  y^2 = 144/(9^2/16+9) = 10.24 = 3.2^2
  y = ±3.2
  x = ±9/16*y = ±1.8
The four points where the slope is ±1 are (±1.8, ±3.2).
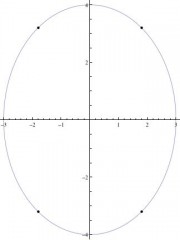If you insist that the rates of change actually be equal, rather than just of equal magnitude, then this will only occur at the two points
  (x, y) = (-1.8, 3.2) or (1.8, -3.2),
that is, those points where the slope is +1.