Sin(15°+x) + Sin(45°-x) = 1
To start solving this problem, you must use the sum-to-product formula* for the addition of two sine terms, where sin(a) + sin(b) = 2sin[(a+b)/2]cos[(a-b)/2]. In this case, the value for "a" is 15°+x and the value for "b" is 45°-x. So let's plug these values in, shall we?
2sin[(15°+x)+(45°-x) /2]cos[(15°+x)-(45°-x) /2] = 1
Simplify the terms inside the parenthesis for both the sine and cosine values. In (15°+x)+(45°-x), since we're adding them, we can directly add 15 with 45 to give 60 degrees. And when we add x with negative x, that just cancels out to 0, so 60 + 0 is still 60. And we're also dividing that entire sum by 2, so 60 divided by 2 is equal to 30 degrees.
2sin(30°)cos[(15°+x)-(45°-x) /2] = 1
For (15°+x)-(45°-x), notice there's some subtraction going on. We're going to distribute that to 45 degrees and -x, like so:
2sin(30°)cos(15°+x-45°+x /2) = 1
Notice how the 45° was originally positive, but turned negative since we distributed negative sign to it as well as to the -x. When you add a negative to something that's already negative, it turns positive, so -x turns into positive x. Now let's combine them.
15° minus 45° turns into -30°, and x+x turns into 2x, so we have 2x - 30°. But we're also dividing that entire difference by 2, so (2x-30°)/2 = x-15°. Now we have:
2sin(30°)cos(x-15°) = 1
Oh look, we have sin(30°) in the equation. Cool, let's check out what the value of it is on the unit circle.
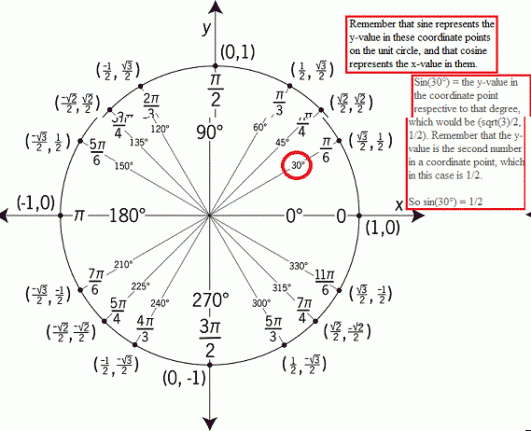
2sin(30°)cos(x-15°) = 1
If we plug in 1/2 for sin(30), we also have to multiply it by 2, so 1/2 * 2 is equal to 1. And 1 times cos(x-15) is just cos(x-15), so we will have:
cos(x-15) = 1
Now think about this, what degree must cosine have to equal exactly to 1? Remember that on a unit circle, the horizontal axis represents values for x. The circle stretches to x values -1 and 1 from left to right, as well as y-values -1 to 1 from bottom to top. Since cosine focuses on x-values, pay attention to the horizontal axis. Where would cosine of anything equal to 1?
Answer: Cosine of something equals to 1 when that something is at 0 degrees, or 360n degrees. You see, when we have cos(0) the coordinate point that's respective to 0 degrees is (1,0), and since we know that cosine focuses on x-values, our answer to cos(0) will be 1. So cos(0) = 1.
Ofcourse, you could always just add 360 to it, because it will give you the same answer. The unit circle expands to a full 360 degrees, so going around the whole circle once will lead you back to where you started. So other valid choices could be cos(360), cos(720), cos(1080), etc. (That's where 360n comes in. The "n" represents how many times you add 360, so it has to be some whole number).
Alright, so let's look back at our equation. We have:
cos(x-15) = 1
So what value does x have to be in order to get cos(0), since we now know that cos(0) = 1? Well it's easy, just set x - 15 equal to 0 and solve for x.
x - 15 = 0
x = 15 (added 15 to both sides)
So x equals to 15 degrees. But remember, you can also add in any amount of 360 to it because it will give you the same answer, since adding 360 degrees will mean you'll go around the entire unit circle once and end up back where you started. So the real answer here is
x = 15° + 360°n