3/5 x (-7 )/8
Examples On How To Find The Product In A Math Problem?
...same answer as before...multiply...product of a and b is a x b
The product of two numbers is the answer you get when you multiply them. I assume you know that, so I assume you are asking how to perform multiplication. The two numbers being multiplied are called factors, or multiplier and multiplicand, or just multiplicands. Most of us do multiplication one of a few different ways. Sometimes the ways are combined. The first step is to recognize that multiplication is a shortcut to the answer of repeated addition. The second step is to memorize a multiplication (times) table. By the time you graduate elementary school, you can be expected to know times tables up to 10 times 10 = 100. Many people know them up to 12 times 12. A times table is shown here. (There is more discussion after the table.) One of the numbers (factors) is found in the left column. The other is found in the top row. The number at the intersection of the corresponding row and column is the product. Example: 2 times 5 is 10. Look at the row with 2 in the left column. Find the column in that row that has 5 in the top row. Of course, you must also know that 0 times any number results in a product of 0.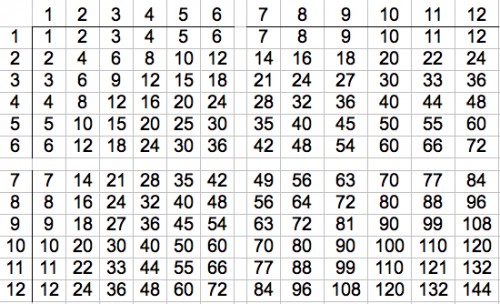 
If you are multiplying more than single-digit numbers, memorizing the times table will not always get the answer for you. There are several ways that students are taught to do multiple-digit multiplication, but they all require you understand place value. The idea is that the value of a digit depends on where it is written with respect to the decimal point (or rightmost digit, if there is no decimal point). Example:
the digit 2 in 246 has a value of 200. This value is 100 times the value of the digit 2 in the number 462. The two zeros in the number 100 correspond to the number of places the digit 2 in 246 is left of the digit 2 in 462. Essentially, we multiply multiple digit numbers a digit at a time. Each digit times digit product is called a partial product, because it is only part of the whole product. We add the partial products together, paying attention to place value, to get the final product. Example: 23*45 We can write one of the factors as the sum of its digit values across the top of the page, and the other one down the side. It might look like this. 40 5 20 3 Now, we can fill in the partial products at the points of intersection of this table. Here's the tricky part. Temporarily forget the zeros on the right. They will be put on the right end of the result from the multiplication table above. Starting with the upper left, we see we need to find the product of 20*40. We know this is just the product 2*4 but with two zeros added. In the times table, we can look up to see 2*4=8, so the the first partial product gets filled in like this: 40 5 20 800 3 Working to the right, our next partial product is 20*5, which we know is 2*5 with a zero added on the right. 2*5 = 10, so 20*5 = 100. We can continue in this fashion to fill in the whole table. 40 5 20 800 100 3 120 15 Now, our multiplication problem has turned into an addition problem. We must find the sum of 800 + 100 + 120 + 15 = 900 + 135 = 1035 We have found that the product of 23 and 45 is 1035.
Some of us learned to do this in a slightly different form. We perform the process of finding partial products and partial sums partly in our head, writing down the result for each digit. Example: 23*45 Would be written as 45 * 23 135 (this is the result of 3*45 = 15 + 120) 90 (this is the result of 2*45 = 10 + 80. [see note]) 1035 [note:
we have written the partial product 2*45 one place to the left, in alignment with the 2 in the factor. This is in recognition that we are really performing 20*45 = 900. We leave space where the 0 would be. You could write it if you want.] There are many subtleties to multiplication. We can perform multiplication by 2 by doubling, for example. (2*135 = 135 + 135 = 270) We can multiply by 9 by multiplying by 10 and subtracting. (9*7 = 10*7 - 7 = 70 - 7 = 63) Once you get into Algebra, you find that sometimes numbers are replaced by letters. Then, multiplication is "indicated" because it cannot actually be performed. We indicate multiplication by writing the letters (variable names) next to each other. Example: Multiply x by itself and multiply that product by 3. The result is 3*x*x. (We usually write the number first.) When the same factor is repeated, we can indicate the repetition with an exponent. An exponent is written in superscript where possible, or using an "exponentiation operator" (^) where plain text must be used. Example: 3*x*x = 3x2 = 3x^2.
the digit 2 in 246 has a value of 200. This value is 100 times the value of the digit 2 in the number 462. The two zeros in the number 100 correspond to the number of places the digit 2 in 246 is left of the digit 2 in 462. Essentially, we multiply multiple digit numbers a digit at a time. Each digit times digit product is called a partial product, because it is only part of the whole product. We add the partial products together, paying attention to place value, to get the final product. Example: 23*45 We can write one of the factors as the sum of its digit values across the top of the page, and the other one down the side. It might look like this. 40 5 20 3 Now, we can fill in the partial products at the points of intersection of this table. Here's the tricky part. Temporarily forget the zeros on the right. They will be put on the right end of the result from the multiplication table above. Starting with the upper left, we see we need to find the product of 20*40. We know this is just the product 2*4 but with two zeros added. In the times table, we can look up to see 2*4=8, so the the first partial product gets filled in like this: 40 5 20 800 3 Working to the right, our next partial product is 20*5, which we know is 2*5 with a zero added on the right. 2*5 = 10, so 20*5 = 100. We can continue in this fashion to fill in the whole table. 40 5 20 800 100 3 120 15 Now, our multiplication problem has turned into an addition problem. We must find the sum of 800 + 100 + 120 + 15 = 900 + 135 = 1035 We have found that the product of 23 and 45 is 1035.
Some of us learned to do this in a slightly different form. We perform the process of finding partial products and partial sums partly in our head, writing down the result for each digit. Example: 23*45 Would be written as 45 * 23 135 (this is the result of 3*45 = 15 + 120) 90 (this is the result of 2*45 = 10 + 80. [see note]) 1035 [note:
we have written the partial product 2*45 one place to the left, in alignment with the 2 in the factor. This is in recognition that we are really performing 20*45 = 900. We leave space where the 0 would be. You could write it if you want.] There are many subtleties to multiplication. We can perform multiplication by 2 by doubling, for example. (2*135 = 135 + 135 = 270) We can multiply by 9 by multiplying by 10 and subtracting. (9*7 = 10*7 - 7 = 70 - 7 = 63) Once you get into Algebra, you find that sometimes numbers are replaced by letters. Then, multiplication is "indicated" because it cannot actually be performed. We indicate multiplication by writing the letters (variable names) next to each other. Example: Multiply x by itself and multiply that product by 3. The result is 3*x*x. (We usually write the number first.) When the same factor is repeated, we can indicate the repetition with an exponent. An exponent is written in superscript where possible, or using an "exponentiation operator" (^) where plain text must be used. Example: 3*x*x = 3x2 = 3x^2.
