Two points are all you need for the linear equation. It is often convenient to choose intercepts.
y = 2x - 18
y = 2(0) - 18 (choose x = 0)
y = -18 (the y-intercept is (0, -18))
0 = 2x - 18 (choose y = 0)
18 = 2x (add 18)
9 = x (divide by 2. The x-intercept is (9, 0))
For the hyperbola, it is usually a good idea to choose at least 3-5 points around the point where the (-3/(2x)) term is equal to 1. You may want to choose values for that term that are ±1/10, ±1/2, ±1, ±2, ±10. These are nicely computed by a spreadsheet.
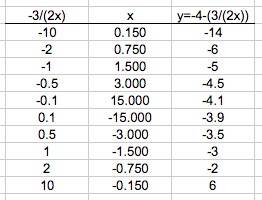The graph using these points looks like ...
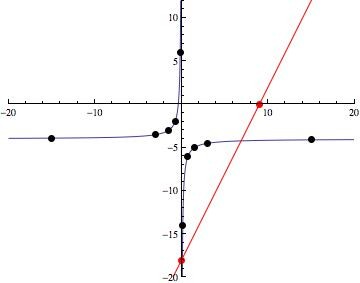
y = 2x - 18
y = 2(0) - 18 (choose x = 0)
y = -18 (the y-intercept is (0, -18))
0 = 2x - 18 (choose y = 0)
18 = 2x (add 18)
9 = x (divide by 2. The x-intercept is (9, 0))
For the hyperbola, it is usually a good idea to choose at least 3-5 points around the point where the (-3/(2x)) term is equal to 1. You may want to choose values for that term that are ±1/10, ±1/2, ±1, ±2, ±10. These are nicely computed by a spreadsheet.
